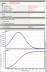
Uncertainty and Sensitivity Analysis - Design Variables

Accessed from Parametric, Optimisation and UA/SA Analysis Settings dialog

Tip: The Edit Variables dialog should be used with caution because there is no Cancel button, so once the dialog is opened, any changes made cannot be undone and upon closing of the dialog, the variable will be saved, replacing the previous one, with the settings currently being shown on the screen. In the case where you have mistakenly added a variable (or made incorrect changes while editing an existing one) you can close the dialog and then delete the incorrect variable on the design variables tab on the main Edit Parametric, Optimisation and UA/SA Analysis Settings dialog. Alternatively if you haven't made any other changes since opening the main dialog , simply press Cancel on that dialog to lose all changes.

Design Variables

The Design variables dialog can be accessed from the Parametric, Optimisation and UA/SA Analysis Settings dialog, when 3-Uncertainty/ Sensitivity Analysis is selected on the Analysis Type Tab, after pressing Add Output or Edit Output.

Name

User defined name for the Design Variable e.g. "Window Wall %"

Variable type

Type of input Design Variable, to be selected from the browse list in the right-hand info panel.

You can view the full list of variable types on the Optimisation - Design Variables section.

Note: All variables are listed for selection regardless of the state of the model so care must be taken to select variables that are appropriate. For example, if the Scheduled natural ventilation model option is used then changes in the % External window opens variable (which only applies to Calculated natural ventilation) won't affect results.

Distribution Category

Type of probability distribution. The category can be selected form the drop-down list. The option selected here (along with analysis level on the Analysis Type tab and Variable Type above) determines the distributions curves available. There are two options:

• 1-Discrete: Available for list type variables and numeric variables.
• 2-Continuous: Available for numeric variables only.

Note: The number of options available for distribution are also controlled by Level selected on Analysis Type Tab.

View the full explanation of Discrete and Continuous categories and their availability in simple and detailed settings.

 

Discrete Distributions: Distribution of the input variable that can take up only finite (or countably infinite) set of values.

Note: When a list type variable is used to modify a single numeric setting within a set of components (e.g. U-value for constructions or glazing) then it is important that the numeric values are evenly spaced in each of the components in the list to ensure meaningful regression sensitivity analysis results. For example if you wish to analyse the effect of changing wall U-value between 0.1 and 0.5 then it is recommended to use a fixed increment in U-value such as 0.1 or 0.05.

Continuous Distributions: Distribution of a random variable that may take any value in a finite or infinite set of values.

Note: If the input variable is a list type one, then it will have a discrete probability distribution. e.g. Constructions assembly options for Wall. If the variable is a numeric type one, it generally will be defined as a continuous distribution, e.g. load power densities or system CoP. However, discrete distribution can also be used for the numeric type variables e.g. Temperature setpoints limited to a discrete increment of 0.5 °C.

The table below lists the various discrete and continuous probability distribution curves available for numeric and list type variables for simple and detailed analysis levels.

 

Analysis Level	Variable Type: Numeric	Variable Type: List
Simple	Discrete Distributions:   3-Binomial 20-Uniform (discrete)	Discrete Distributions:   3-Binomial 20-Uniform (discrete)
	Continuous Distributions:   12-Log-Normal 14-Normal 18-Triangular 19-Uniform	Continuous Distributions:   Not Applicable
Detailed	Discrete Distributions:   3-Binomial 20-Uniform	Discrete Distributions:   1-Bernoulli 3-Binomial 9-Geometric 10-Hyper-Geometric 13-Negative Binomial 16-Poisson 20-Uniform
	2-Beta 4-Cauchy 5-Chi-Squared 6-Exponential 7-Fischer F 8-Gamma 11-Levy 12-Log-Normal 14-Normal 15-Pareto 17-Student T 18-Triangular 19-Uniform 21-Weibull	Continuous Distributions:   Not Applicable

Distribution Curve

The statistical function that describes the possible values and their likelihoods for the Design Variable. Select the distribution Curve from the drop-down list.

View the full list of all distribution curves: and links to Wikipedia Pages

 

S.No.	Distribution (hyperlink to Wiki pages)	Category (Discrete / Continuous	Analysis Level (Simple / Detailed)	Sample Image	Controlling Parameters
1	Bernoulli	Discrete	Detailed	NA	Probability of Second option   (Can only have 2 variable value options)
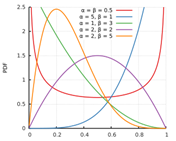
2	Beta	Continuous	Detailed		Left shape parameter (Alpha)   Right shape parameter (Beta)
3	Binomial	Discrete	Both		Number of Trials (n)   Probability (p)
4	Cauchy	Continuous	Detailed		Scale Parameter   Location (Peak Value)
5	Chi Squared	Continuous	Detailed		Degree of Freedom
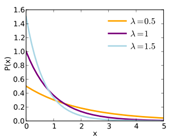
6	Exponential	Continuous	Detailed		Mean
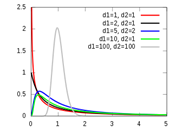
7	Fisher F	Continuous	Detailed		Degree of Freedom (n)   Degree of Freedom(d)
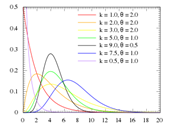
8	Gamma	Continuous	Detailed		Shape parameter   Scale parameter
9	Geometric	Discrete	Detailed		Probability (p)
10	Hypergeometric	Discrete	Detailed		Population size   Population Number   Sample Size
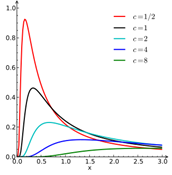
11	Levy	Continuous	Detailed		Min Val (Location Parameter)   Scale parameter
12	Log Normal	Continuous	Both		Mean   Standard Deviation
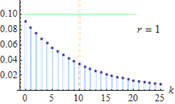
13	Negative Binomial	Discrete	Detailed		Number of success   Probability
14	Normal	Continuous	Both		Mean   Standard Deviation
15	Pareto	Continuous	Detailed		Shape parameter   Scale parameter
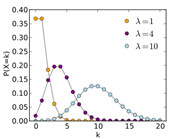
16	Poisson	Discrete	Detailed		Mean
17	Student T	Continuous	Detailed		Degree of Freedom (n)
18	Triangular	Continuous	Both		Location (Peak Value)   Min Val   Max Val
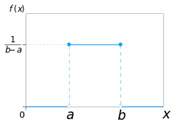
19	Uniform (Continuous)	Continuous	Both		Min Val   Max Val
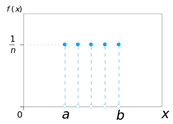
20	Uniform (Discrete)	Discrete	Both		Min Val   Step Size   Number of Steps
21	Weibull	Continuous	Detailed		Shape parameter   Scale parameter

Distribution Parameters

Depending on distribution curve various distribution parameters are available.

View the full list of all distributions and their controllers

 

SNo.	Distribution	Parameters	Limitation	Example Case	Example Image
1	Bernoulli	Probability of Second option	Value Between 0 and 1	Variable: Glazing Template   Variable options selected: 2   Probability of Second option = 0.7
2	Beta	Left shape parameter	>0, Real Number, up to 50	Variable: Boiler CoP   Left shape parameter = 9   Right shape parameter = 3
		Right shape parameter	>0, Real Number, up to 50
3 A	Binomial for List type variables	Probability	Value Between 0 and 1	Variable: Glazing Template   Variable options selected: 5   Probability = 0.5
		Number of Trials	Locked
3 B	Binomial for Numeric type variable	Probability	Value Between 0 and 1	Variable: % External Window Opens   Probability = 0.6   Number of trials = 10
		Number of Trials	Positive Integer
4	Cauchy	Scale Parameter	>0, Real Number up to 10	Variable: Window Wall %   Scale Parameter = 5   Location = 50
		Location (Peak Value)	Real Number
5	Chi Squared	Degree of Freedom (n)	Positive Integer up to 100	Variable: Equipment Power Density   Degree of Freedom (n) = 15
6	Exponential	Scale Parameter	>0, Real Number up to 5	Variable: Miscellaneous Power Density   Scale Parameter = 3
7	Fisher F	Degree of Freedom (n)	>0, Real Number up to 5	Variable: Infiltration rate   Degree of Freedom (n) = 40   Degree of Freedom (d) = 90
		Degree of Freedom (d)	>0, Real Number up to 5
8	Gamma	Shape Parameter	>0, Real Number up to 20	Variable: Equipment Power Density   Shape Parameter = 5   Scale Parameter = 2
		Scale Parameter	>0, Real Number up to 5
9	Geometric	Probability of first option	Value Between 0 and 1	Variable: Glazing Template   Variable options selected: 5   Probability of first option = 0.5
10	Hypergeometric	Number of trials	locked for list type variables	Variable: Glazing Template   Variable options selected: 5   No of successes = 50
		Size of population	locked for list type variables
		No of successes	Value between no of trials & (Size of population – dumber of trials)
11	Levy	Scale Parameter	>0, Real Number up to 10	Variable: Infiltration rate   Scale Parameter = 0.2   Min Value = 0.5
		Min Value	Real Number
12	Log Normal	Mean	Real Number	Variable: Infiltration rate   Mean = 0   Standard Deviation = 0.5
		Standard Deviation	>0 value
13	Negative Binomial	Probability	Value Between 0 and 1	Variable: Glazing Template   Variable options selected: 5   Probability = 0.5   No of trials = 3
		No. of trials	Positive Integer up to 10
14	Normal	Mean	Real Number	Variable: Window Wall %   Mean = 40   Standard Deviation = 10
		Standard Deviation	>0 value
15	Pareto	Shape Parameter	>0, Real Number up to 50	Variable: Miscellaneous Power Density   Shape Parameter = 1   Scale Parameter = 3
		Scale Parameter	>0, Real Number up to 50
16	Poisson	Mean	>0, Real Number up to 50	Variable: Glazing Template   Variable options selected: 5   Mean = 2.5
17	Student T	Degree of Freedom (n)	Positive Integer up to 100	Variable: Cooling setpoint PMV   Degree of Freedom (n) = 100
18	Triangular	Location (Peak Value)	Between Min and Max	Variable: Window Wall %   Location (Peak Value) = 60   Min Value = 20   Max Value = 80
		Min Value	Real Number less than Max Val
		Max Value	Real Number more than Min Val
19	Uniform (Continuous)	Min Value	Real Number less than Max Val	Variable: Window Wall %   Min Value = 20   Max Value = 80
		Max Value	Real Number more than Min Val
20 A	Uniform (Discrete) for List type variable	No parameters to control	NA	Variable: Glazing Template   Variable options selected: 5
20 B	Uniform (Discrete) for Numeric type variable	Min Value	Real Number less than Max Val	Variable: Window Wall %   Min Value = 20   Distribution Seep size = 10   Number of steps = 6
		Max Value	Locked
		Distribution Seep size	>0, Real Number
		Number of steps	>0 Integer value
21	Weibull	Shape Parameter	>0, Real Number up to 50	Variable: Infiltration Rate   Shape Parameter = 3   Scale Parameter = 1.25
		Scale Parameter	>0, Real Number up to 50

Transform Distribution

Functions under this header can be used to control the distribution curve value ranges to have more meaningful values to adapt to the variable type. This allows you to use curves whose default values are not necessarily in line with the Input Variable. These are only available for numeric distributions.

Shifting and Scaling: Depending on the operator selected, the value range of the default graph is either shifted or scaled or both.

Truncation: To avoid improbable or conflicting values being sampled, truncation can be used to remove the tales of the distribution.

Shift/Scale Value Range

Operator

There are 4 Options:

• 1-Shift only: adds Shift value to each untransformed distribution (x+a)
• 2-Scale only: multiplies scale value to each untransformed distribution (x*b)
• 3-Shift then Scale: adds Shift value and then multiplies scale value to each untransformed distribution (x+a)*b
• 4-Scale then Shift: multiplies scale value and then adds Shift value to each untransformed distribution (x*b)+a

Shift value

Enter the value which is added to the default distribution’s numbers.

Note: When using IP units, for variables with units, the shifting of the distribution is controlled by a shift slider. The values can be increased or decreased by moving the slider right or left respectively. The effect of the shift slider setting on the distribution should be checked by looking at the graph at the bottom of the dialog. See screenshot under Scale value below.

Scale value

Enter the value which is multiplied to the default distribution’s numbers.

Note: When using IP units, for variables with units, the scaling of the distribution is controlled by a scale slider. The graph values scale up or down on moving the slider right or left respectively. The effect of the scale slider setting on the distribution should be checked by looking at the graph at the bottom of the dialog.

The screenshot below illustrates a case where cooling setpoint temperature distribution is controlled using the Beta distribution with slider controls and lower and upper truncation when using IP units.

Truncate Lower side

Limit:

This value removes all the variable values below this number. In this case the probability which is removed is redistributed across the remaining curve. The value should be more than the minimum value in the untruncated graph and less than truncation upper side limit.

Truncate Upper side

Limit:

This value removes all the variable values above this number. In this case the probability which is removed is redistributed across the remaining curve. The value should be less than the maximum value in the untruncated graph and more than the truncation lower side limit.

The value should be less than the maximum value in the untruncated graph and more than the truncation lower side limit.

View the full list of all distributions and transformations available

 

	Distribution	Transformations available	Example Image
2	Beta	Shift/Scale
		Truncate Lower Side
		Truncate Upper Side
4	Cauchy	Shift/Scale
		Truncate Lower Side
		Truncate Upper Side
5	Chi Squared	Shift/Scale
		Truncate Lower Side
		Truncate Upper Side
6	Exponential	Shift/Scale
		Truncate Lower Side
		Truncate Upper Side
7	Fisher F	Shift/Scale
		Truncate Lower Side
		Truncate Upper Side
8	Gamma	Shift/Scale
		Truncate Lower Side
		Truncate Upper Side
11	Levy	Shift/Scale
		Truncate Lower Side
		Truncate Upper Side
12	Log Normal	Shift/Scale
		Truncate Lower Side
		Truncate Upper Side
14	Normal	Truncate Lower Side
		Truncate Upper Side
15	Pareto	Shift/Scale
		Truncate Lower Side
		Truncate Upper Side
17	Student T	Shift/Scale
		Truncate Lower Side
		Truncate Upper Side
18	Triangular	N/A
19	Uniform (Continuous)	N/A
21	Weibull	Shift/Scale
		Truncate Lower Side
		Truncate Upper Side

Warning when changing from SI to IP units: If any variables that were defined in SI units are edited, the transformations (shifting/scaling and truncations) will be reset.

Variable Values

Options list

The Options list is only available for list type variables. It allows you to select non-numeric options and create a list of various variables that will be sampled from during the UA/SA.

Click on the browse button to open a list of components or templates for selection. In the new Select design option window, items can be selected by checking the appropriate checkboxes.

The number of items selected form the discrete distribution’s items and truncates the distributions selected (if required).

After selecting the options, it is important to order the list, to match the unintended probability values of each of the section. This is done in the Variable Option Order dialog which is automatically displayed after adding/editing a list of variable options.

Important Note: The selection order must be set up to ensure that SA can assess the effect of incremental changes to values of the selected options on the main output of interest. For example, if the variable is wall construction with each construction having a different U-value (perhaps by varying insulation thicknesses), and if building heating energy is the SA output, then the constructions should be ordered based on (increasing or decreasing) U-value . This is because U-value is the construction attribute that has the greatest influence on heating energy. If you do not take care to order option lists in this way, then the SA results will not be meaningful. See also: Running Sensitivity Analysis as a Precursor to Optimisation.

Target

Target objects

This setting allows you to select one or more object(s) to which the variations are to be applied. The object(s) you select here are the places in the model where the variations will be applied. Normal model data inheritance rules apply so if you set the building as the target then the change will set for the building but will also inherit down to block, zone, surface and opening levels where appropriate. In this case any hard-set data at block or lower levels will prevent inheritance in the normal way.

Tip: For models imported via gbXML any construction or glazing assignments are set in the DesignBuilder model at surface level and so the normal inheritance paths used for construction and glazing will be overriden. Therefore in this case, if you need to parametrically adjust construction or glazing surface properties you may need to apply the changes to each surface individually by selecting the appropriate surfaces as targets.

Graph

This is the visual representation of the probability curve and shows the probability distribution curve/ probability mass curve and cumulative distribution curve. To update the graph to display the current settings click on the Create/Update Graph button.