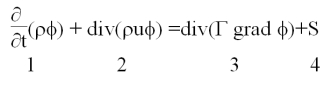
The numerical method used by DesignBuilder CFD is known as a primitive variable method, which involves the solution of a set of equations that describe the conservation of heat, mass and momentum. The equation set includes the three velocity component momentum equations (known as the Navier-Stokes equations), the temperature equation and where the k‑e turbulence model is used, equations for turbulence kinetic energy and the dissipation rate of turbulence kinetic energy. The equations comprise a set of coupled non-linear second-order partial differential equations having the following general form, in which f represents the dependent variables:
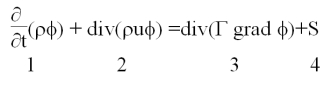
Term 1 represents the rate of change, term 2 represents convection, term 3 represents diffusion and S is a source term.
Due to its non-linearity, the equation set cannot be solved using analytical techniques, which necessitates the requirement for a numerical method. The numerical method employed by DesignBuilder involves re-casting the differential equations into the form of a set of finite difference equations by sub-dividing the required building space (or calculation domain) into a set of non-overlapping adjoining rectilinear volumes or cells, which is collectively known as a finite volume grid. The equation set is then expressed in the form of a set of linear algebraic equations for each cell within the grid and the overall set of equations is solved using an iterative scheme. The non-linearity of the equation set is accounted for by the use of a nested iterative scheme whereby each dependent variable equation set (velocity components, temperature, etc.) are themselves solved iteratively within an overall outer iterative loop and at the termination of each outer iteration, the most recent values of the dependent variables are fed back into the dependent variable coefficients. The outer iterative loop is repeated until the finite difference equations for all cells are satisfied by the current values of the appropriate dependent variables, at which point the scheme is said to have ‘converged’. An appreciation of the requirement for convergence and the nested iterative procedure used to achieve it will help in understanding the meaning of the various calculation options that are described in the ‘Conducting CFD Calculations’ section.
The calculation procedure has been developed to ensure that the iterative solution of the equation set would be guaranteed to converge if the equation coefficients were constant. However, the equation set is non-linear and the coefficients actually contain the dependent variables themselves, and consequently convergence cannot be guaranteed in all cases. Although in the majority of cases, as long as the dependent variables and particularly the velocities only change slowly, a converged solution is normally achieved.
The main mechanism to ensure that the variables change slowly is that of false time steps. The finite difference equation set is formulated in the form of a transient equation set although the calculations are steady state, i.e. essentially a ‘snap-shot’ in time. The reason for this formulation is that the transient term behaves as a very effective relaxation method, which can slow the change in dependent variables in order to arrive at a more stable solution. The false time step is the time step used in the pseudo-transient term of the dependent variable equation.
CFD calculation uses the so-called Boussinesq approximation that assumes the flow is incompressible except in the case of the buoyancy source term.
Tip: You can find more details on the calculation method used in the CFD Technical online document.