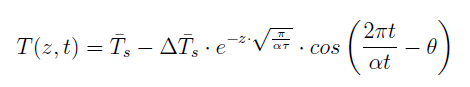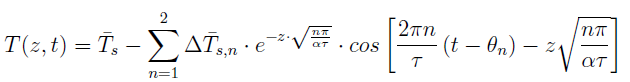Ground Domain - Ground Undisturbed Temperatures
Ground Undisturbed Temperature tab on Ground Domain Dialog.
During the simulation EnergyPlus needs to have access to the distribution of temperatures in the "undisturbed" ground at the site. This means the temperature that would exist in the ground over the year if the building(s) were not present. EnergyPlus provides three ways to calculate these undisturbed ground temperatures:
More information on these options is provided below. Note that all of the calculation methods also require the ground thermal properties as defined by the soil material on the Soil tab.
Finite Difference
The Finite Difference method uses a 1-D finite difference heat transfer model which uses the weather file to obtain surface boundary conditions. An annual simulation is run on the ground model during it’s initialization until the annual ground temperature profile has reached steady periodic behaviour. Once steady periodic behaviour is reached, the ground temperatures are cached for retrieval during the rest of the simulation.
No additional data needs to be entered for this option.
 Technical
Technical
This model uses a 1-D implicit finite difference heat transfer model to determine the steady periodic annual ground temperature. The model, which uses a daily timestep, is run through an annual simulation using the user provided weather file to determine daily averages for global horizontal radiation, air temperature, relative humidity, and wind speed. Once the steady-periodic ground temperature has been determined, the temperatures are cached for use later in the simulation. The basis for the model was taken from Xing, 2014, however, the numerical methods were adapted from those described in Lee, 2013; the latter uses an implicit numerically stable finite difference method, whereas the former utilized an explicit, conditionally stable method. Surface heat balance boundary conditions are similar what is described in Herb et al., 2008. Evapotranspiration is considered as described by Allen et al., 1998. Soil freezing given the assumed stagnant soil moisture content is also considered. The model does not consider the effects of vegetative canopy layers, snow cover, ground water flow, ground moisture transport, or surface runoff.
Kusuda-Achebach
The Kusuda-Achebach method provides an undisturbed ground temperature based on the correlation developed by Kusuda T. and P. Achenbach. 1965. The correlation uses three parameters for ground temperature at the surface to define a correlation for undisturbed ground temperatures as a function of depth and time. If one thinks of the ground temperature for a given depth as a sinusoid, the average ground temperature, amplitude (average difference between maximum ground temperature and minimum ground temperature), and the phase shift (day of minimum surface temperature) are all required to define the correlation.
 Technical
Technical
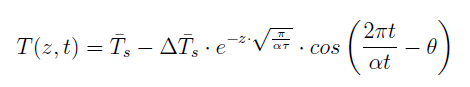
Where:
T(z, t) is the undisturbed ground temperature as a function of time and depth.
Ts is the average annual soil surface temperature, in °C.
Δ Ts is the amplitude of the soil temperature change throughout the year, in °C.
ϴ is the phase shift, or day of minimum surface temperature.
α is the thermal diffusivity of the ground.
τ is the time constant, 365.
Kusuda-Achebach annual average ground surface temperature
The average ground surface temperature throughout the entire year (in °C or °F)
Kusuda-Achebach average amplitude of annual ground surface temperature
The average amplitude of the ground surface temperature (in °DeltaC or °DeltaF)
Kusuda-Achenbach phase shift of minimum surface temperature
The day of the year which has the lowest ground surface temperature (in days).
Xing
This model uses the correlation developed by Xing, 2014 to predict undisturbed ground temperature. The correlation is a 5 parameter, 2 harmonic model based on the work of Lord Kelvin (Thomson, 1862). The average soil surface temperature and two sets of surface temperature amplitude and phase shift must be provided.
 Technical
Technical
Parameters for 4000+ international locations can be found in Xing, 2014. Thomson, W. 1862. ‘On the Reduction of Observations of Underground Temperature, with applications to Professor Forbes’ Edinburgh Observations and the continued Calton Hill Series.’ Proceedings of the Royal Society of Edinburgh. IV: 342-346. Xing, L. 2014. Estimations of Undisturbed Ground Temperatures using Numerical and Analytical Modeling. Ph.D. Diss. Oklahoma State University, Stillwater, OK.
The parameters were first determined by creating and validating a finite difference numerical model which used local weather data for boundary conditions. From the numerical model, the correlation parameters were determined to provide for this simplified design model.
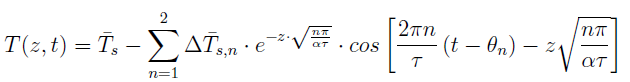
Where:
T(z,t) is the undisturbed ground temperature as a function of time and depth
Ts is the average annual soil surface temperature, in deg C
Δ Ts,n is the n-th amplitude of the soil temperature change throughout the year, in °C
n is the n-th phase shift, or day of minimum surface temperature
α is the thermal diffusivity of the ground.
τ is the time constant, 365.
Average soil surface temperature
The average annual surface temperature of the soil (in °C or °F).
Soil surface temperature amplitude 1
First soil surface temperature amplitude parameter (in °C or °F).
Soil surface temperature amplitude 2
Second soil surface temperature amplitude parameter (in °C or °F).
Phase shift of surface temperature amplitude 1
Phase shift of surface temperature amplitude 1, in days.
Phase shift of surface temperature amplitude 2
Phase shift of surface temperature amplitude 2, in days.